My View on Differential Privacy

Since last April, when I was introduced to the deep pit of differential privacy (DP) by a senior, it has been almost a year now. During this year, I have been immersed in reading papers, brainstorming ideas, coding experiments, and writing papers on my own. I have taken quite a few detours and stumbled several times in various pitfalls. Ultimately, I completed a small paper, and I am somewhat inclined to bid farewell to differential privacy and seek other research directions that are more engineering-oriented and empirical.

Before saying goodbye to differential privacy, please allow me to review the image of differential privacy in my mind~

Overall, differential privacy is a theoretically strong concept. It is not as much of a "black box" as deep learning, nor is it as clear and intuitive as other engineering privacy protection mechanisms (such as the Tor network). Instead, it relies on strictly defined models and provable probabilistic constraints to achieve privacy protection.

Differential Privacy#

Differential privacy guards against differential attacks, which originated in the database field and describes a process by which an attacker infers specific changes in the data within a database.

Model#

Consider two parties:

Database curator: He possesses a complete database (e.g., a relational database), where each entry contains personal information about a user. He only provides an aggregation query interface (function) $f$ (e.g., count, sum, max) to third parties.
Attacker: Based on existing knowledge, attempts to query the database through the interface provided by the curator to learn about individual records.

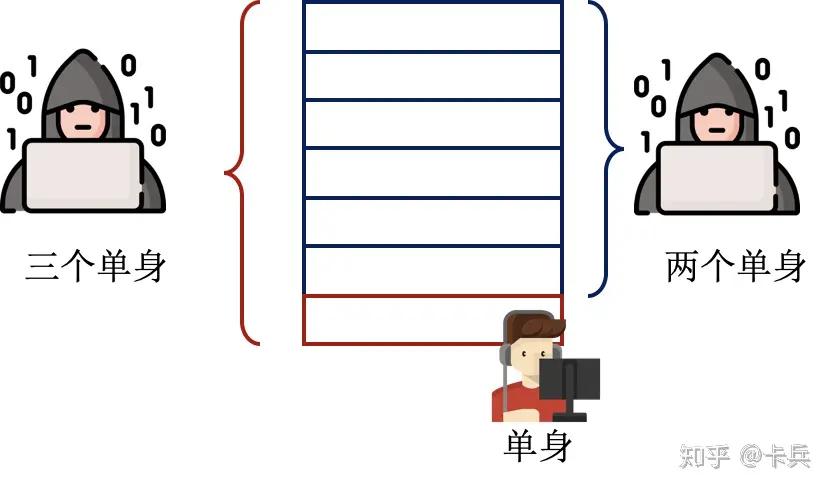
For example, there is a table recording users' names and genders, such as: <Alice, Female>. The curator provides an interface to query the number of Males and Females:

The attacker queries the number of Males once.
At this point, the data table changes, adding a record <Bob, Male>. Note: Assume the attacker knows that Bob has been added to the database but does not know his gender. The attacker wants to know this information.
The attacker queries the number of Males again, and by taking the difference between the two query results, he can determine Bob's gender.

A similar example is provided in the popular science article Introduction to Differential Privacy on Zhihu.

Definition#

There are various views on the definition of privacy, one common interpretation is to "hide specific users in the crowd." For example, the classic k-anonymity algorithm requires that there be at least k records with the same value within a set. The requirement of differential privacy is similar, but it demands that the probabilities of the random algorithm's input and output are close.

(differential privacy) Given any two adjacent datasets $X$ and $X'$ (adjacent can refer to the case assumed above where only one user data is inserted, of course, there are other more abstract interpretations), a random algorithm $\mathcal{M}$ satisfies $\epsilon$-differential privacy ($\epsilon$-DP) if for any possible result $y$, it holds that

\frac{\Pr[\mathcal{M}(X)=y]}{\Pr[\mathcal{M}(X')=y]}\leq e^\epsilon

In short, differential privacy requires that the probabilities of returning the same result are close. Clearly, the aggregation function $f$ (count, sum, max) mentioned above corresponds to $\mathcal{M}$ here, but the results provided by the aggregation function are deterministic and do not contain randomness, thus they do not satisfy $\epsilon$-DP.

Similar to k-anonymity, differential privacy provides a definition of privacy, and how to achieve differential privacy requires researchers to design the algorithm $\mathcal{M}$.

Mechanism#

Transforming $f$ is actually quite simple; it only requires adding some randomness during the computation of the function. In fact, almost all differential privacy protection mechanisms $\mathcal{M}$ revolve around the core of "adding randomness."

Common methods for adding randomness mainly fall into two categories:

Adding random noise to variables, such as Laplacian noise or Gaussian noise, i.e.,

\mathcal{M}(X)=f(X)+\eta,\ \eta\sim Laplacian(\frac{\Delta f}{\epsilon})

where $\Delta f$ represents the sensitivity of $f$, indicating the maximum difference of $f$ under any two distinct $X$.

Using random response, which decides the program's execution flow by flipping a coin, akin to a random if-branch statement.

Properties#

Differential privacy has certain properties that facilitate the combination and extension of existing algorithms to form new differential privacy perturbation algorithms.

Properties

Local Differential Privacy#

Model#

To ensure that users' privacy is guaranteed by differential privacy, these curators need to modify the algorithm and add randomness. In real life, database holders (curators) are often service-providing companies, and it is unrealistic to trust them to protect users' privacy; it is already good enough that they do not sell complete data to third parties~

Therefore, researchers proposed a stricter requirement—local differential privacy (LDP). It considers everyone except oneself as a potential attacker, including the curator.

(local differential privacy) Given any two arbitrary data $x$ and $x'$ (here it is no longer two adjacent datasets, as a single user corresponds to a single record), a random algorithm $\mathcal{M}$ satisfies $\epsilon$-local differential privacy ($\epsilon$-LDP) if for any possible result $y$, it holds that

\frac{\Pr[\mathcal{M}(x)=y]}{\Pr[\mathcal{M}(x')=y]}\leq e^\epsilon

The biggest difference from DP is that LDP imposes requirements on the algorithm $\mathcal{M}$ on the client side. In the DP model, the data reaching the database is the user's real data, while in the LDP model, the data sent by the user has already been processed by $\mathcal{M}$ into pseudo data (i.e., the $y$ in the formula).

Clearly, LDP is more likely to satisfy users who require privacy protection because, in the entire universe, no one knows the real data except for themselves.

Privacy Utility Tradeoff#

Privacy and utility are two relative concepts, representing opposite ends of a scale. Utility reflects the value of the data for use. When user data is modified for privacy protection purposes, it can introduce bias, thereby affecting service quality. For example, in location-based service (LBS) applications, users need to upload their geographical location to enjoy services (like food delivery, ride-hailing, navigation). When the service provider can only offer services based on the pseudo location uploaded by the user, it can lead to some troubles (e.g., food being delivered to the wrong location).

Therefore, ensuring both privacy and minimal utility loss becomes particularly important, which is a core issue to consider in privacy research. In academic papers, it is necessary to conduct theoretical analyses of the benefits of privacy and the losses of utility, as well as to define metrics to empirically evaluate the changes in both.

For utility, specific utility metrics depend on the type and usage of the data.

Numerical data
- Calculating averages and other statistics.
- Interval statistics (histograms).
Categorical data
- Frequency statistics.
- Finding the most frequent category (the majority category).
(Other) Location data
- Nearby PoI (restaurants, parks, hotels, etc.) queries.
- Location services.

The calculation of utility loss varies for different applications and needs to be analyzed on a case-by-case basis. Often, an algorithm that can ensure that the utility loss in a specific application scenario is not too great while guaranteeing privacy is already quite good. Of course, the measurement of loss should not be in absolute terms; it can be relative sizes of different algorithms or measured using a factor (similar to asymptotic complexity).

Application#

The application of LDP is quite aligned with user experience in the mobile internet era. General users are usually aware that service providers are not very trustworthy, so it is safer if protective measures are implemented on the client side. Some technically skilled users may even test whether the data sent from the client has been processed (e.g., through packet capturing).

Apple Emoji

Some software service companies collect user usage data to improve their service quality. More reputable large companies may pop up a dialog box asking, "Do you allow the collection of anonymous usage data?" for users to choose. This data can be used to analyze information such as the usage frequency of specific features. For example, Apple collects statistics on Emoji usage frequency and provides an annual report covering all users. This process can be abstracted as a statistical process for categorical data. To ensure that users' privacy in using Emojis is protected by differential privacy, Apple performs some very complex processing on the data both locally and on the server. The specific process is published in Learning with Privacy at Scale - Apple Machine Learning Research.

Apple

Additionally, Google has also released its LDP application plan RAPPOR.

Rappor

The client-side portions of the LDP plans from these two major companies are quite similar and can be summarized in two points:

First, use a hash function to encode the original data into a binary string.
Use random response to flip each binary bit.

Of course, after these processing steps, a single piece of data often becomes "unrecognizable," but when a large amount of unrecognizable data is collected by the server, the service side can use certain algorithms to obtain estimates that are relatively close to the true values (frequency, histograms, etc.).

Currently, research literature indicates that LDP has been applied in production environments by Google, Apple, and Microsoft, which is also one of the drawbacks of LDP—achieving good utility requires a massive amount of data.

Location Privacy

Geo DP

Another common application of LDP is in geographic location services. Within the framework of LBS, LDP requires that the probability of any two locations being confused to the same location is similar. However, making the probabilities of two locations in Beijing and London being confused to Shanghai similar would result in significant utility loss. Therefore, a common approach, as described in the paper Geo-Indistinguishability, is:

\frac{f(z|x)}{f(z|x')}\le e^{\epsilon d(x,x')}

The similarity of probabilities is directly related to the distance between the two locations. Thus, all locations within a radius of r centered on the user's true location can be viewed as an equivalence class, where each location in this equivalence class has a probability close to being confused with the user's true location, which is the so-called "fuzzy location" range in the above image.

Inference Attack#

When discussing DP, one cannot overlook inference attacks. An attacker, based on existing prior knowledge $\pi$ and the publicly available confusion mechanism $\mathcal{M}$, infers the possible distribution of the user's real data. It is important to note that (L)DP does not prevent inference attacks because inference attacks assume that the attacker possesses $\pi$, while DP is completely independent of $\pi$. In fact, the advantage of DP lies in its applicability under any $\pi$. If the attacker has already mastered the real data, i.e., $\pi(x_0)=1$, then no matter how stringent the DP requirements are, the attacker can still provide the correct answer.

The role of DP is that, based solely on $\mathcal{M}$ itself, the attacker cannot gain any additional information (information gain). Because the confusion of data by $\mathcal{M}$ is random and the randomness is relatively "uniform," the attacker cannot accurately reverse-engineer the real data based solely on $\mathcal{M}$. However, this does not mean that the attacker cannot accurately reverse-engineer the data using other information.

Several papers have analyzed the limitations of differential privacy in specific application scenarios, such as in geographic location privacy protection, including:

Inability to resist inference attacks: as in PIVE.
Extreme utility loss due to randomness: as in Back to the Drawing Board.

How to Water Paper#

Based on my understanding of academic research related to DP, the difficulty of DP-related papers decreases in the following order:

Proposing a new DP model (scheme) or foundational method, such as shuffle model, amplification by resampling, vector DP, etc. Writing such papers requires strong mathematical skills and the derivation of various upper and lower bounds.
After uncovering the flaws of DP, combining DP with other privacy protection concepts. This type of problem usually tests the understanding of privacy and utility.
Introducing DP into specific applications, such as LBS, crowd sensing, federated learning, etc., using it as a constraint for optimization problems or improving existing engineering practices through more advanced DP models, supplemented by theoretical analysis (formulas).

Summary#

DP is a concept with strong theoretical foundations, imposing strict constraints on the randomness of the data processing process $\mathcal{M}$, requiring that the probabilities of returning the same output for any two inputs are close. Compared to other privacy concepts, DP is more difficult for users to understand, and providing a clear and intuitive explanation of the privacy protection effects (including changes with parameters) is quite challenging.