DFA#
一个正规语言(Regular Language)的语法可以用一个正则表达式(Regular Expression)来描述,或者用一个确定有限自动机(Definite Finite Automation,DFA)来表达,例如:
一个仅包含字符 a 和 b,且他们各自出现次数均为偶数的字符串。
可以表示为
其中 q0 既是起始态,也是终结态。
如果将该 DFA 视为一个黑盒,用户输入一个字符串之后仅能够得到该字符串是否符合该文法的布尔值(accept /reject),那么通过不断的尝试符号的组合,并且根据是否符合文法的判断来反向推断文法 / DFA,就可以看作是学习状态模型(state model)的过程。
Definitions, Notations#
一个 DFA 由五元组 表示:
- 是有限的所有可能出现的状态集合。
- 是有限的所有可能出现的符号集合。
- 是状态转移规则:在某个状态下输入某个符号,自动机会跳转到下一个状态。
- 是终结状态的集合。
- 是初始状态。
Observation Table, OT#
L* 算法的核心是一张表 ——Observation Table(OT),一个 OT 可以表示为三元组 $(S_D,E_D,T_D)$:
- 包含前缀封闭的字符串集合,是表格的行索引的一部分。这些字符串表示可能存在的状态,被称作 access string。
- 包含后缀封闭的字符串集合,是表格的列索引的集合。这些字符串用于区分不同的状态(即定义状态的等价关系),被称作 distinguish string。OT 中任意取出两行 $s,t$,若他们对应的每个 distinguish string 的项的取值都相等(也就是说这两行的内容完全相同),那么这两行对应的状态就是等价的,记作 。等价的状态可以被归并为 1 个状态,在 DFA 中表示为 1 个节点。
- : 表示表中每行每列的项。其中行索引不仅包含 ,还包含 ,后者为每个可能的 后加上一个符号组成的字符串的集合。 的取值由字符串 (直接相连) 能否被 accept 决定,是一个布尔值。
- OT 表中真正表示状态的行为 , 跟多的只是用于辅助判断状态之间跳转关系的。
要使得 OT 能够表示成一个合理的 DFA,需要满足两个性质:
- 封闭性(closed):因为 表示从一个状态出发,添加一个符号,到达的下一个状态,这个新的状态如果与 所有 中的状态都不等价,那就说明存在至少一个新状态,即 OT 不封闭,还可以继续拓展。将来在构造 DFA 时,就知道每一个状态 添加任意一个符号 之后会跳转到的目的状态,如果目的状态已经存在在 中了,那无妨,但如果不存在在 $S_D$ 中,那就说明还有新的状态没有探索到。
- 一致性(consistent):对于任意两个等价的状态 ,对于每一个符号 ,都要有 。如果不成立,那就说明 s、t 不是等价的,因为从他们出发通过同一个符号可能会到达不同的状态。等价关系根据当前 OT 的列索引(distinguish string)产生,因此在列索引产生变化之后等价关系同样也会发生变化。一般而言,对与一个状态的认识是从模糊到精确的过程,所以先前被认为是等价的关系往往随着 distinguish string 的增加会变为不等。
L* Algorithm#
- 初始化 ,并且连同 一道构造 OT 的所有行。
- 为了获得每一行的项的取值,向 oracle 进行 membership query:对于 ,询问 oracle 从状态 s 出发经过符号 e 的路径是否能够 accept。填充整张表。
- 判断是否为封闭和一致:
- 如果不封闭,就从 中取出一个不封闭的行,移动到 部分。
- 如果不一致,即 , 就将 加入到 distinguish string 中。横向拓展 OT,并通过 membership query 填充表内内容。
- 如果一致,通过 OT 构造 DFA,向 oracle 提出 equivalence query(等价查询):
- 如果不等价,oracle 会返回 counter example(反例),将反例的所有前缀 string 添加到 中,并拓展 ,回到步骤二。
- 如果等价,那么就结束了。
Example#
Reverse Engineering Enhanced State Models of Black Box Software Components to support Integration Testing 给出的例子的完整过程如下。假设 oracle 有如下的 DFA。

其 , 为 加上 中的每个符号(),初始状态 。

- 该 OT 既是一致的,但不封闭,因为 在 中没有与其等价的行(),因此把 (即 )移入 中。
- 由于 a 被新添加到了 ,所以 需要添加 ,对 oracle 做 membership query,得到 。
- 此时 OT 是封闭且一致的,且只有 2 个等价类,一类是 ,另一类是 ,这两个等价类反映到图上就是 2 个状态,并且结合后一个类上添加字符 a 和 b 到达的不同的状态,可以得到 DFA。

- 此时做等价查询,得到反例 没有被构造出的 DFA 满足。将 的所有前缀()添加到 OT 的 中,并且将 加入到 。

- 此时 OT 是否封闭的,但不一致,因为等价状态 添加同一个符号 后的 ,说明 实际上并不等价,需要做进一步区分,区分的依据即为状态 再添加一个符号 之后可能跳转的状态。
- 添加了 之后,对 oracle 做 membership query,填满整个 OT,上一个 OT 中等价的 a、b 此时也已经不等价了。
- 此时 OT 是一致且封闭的,可以构造成 DFA。

- 对 oracle 做 equivalence query,得到反例 虽然是构造出的 DFA 所能 accept,但是 oracle 对其 reject。将 的所有前缀加入 (这里只需要再添加 即可),并且向 添加 。

- 此时 OT 是封闭但不一致的,因为 ,则需要把 也加入 ,横向拓展 OT。
- 对 oracle DFA 做 membership query,填充整张表,此时表式封闭且一致的,构造出的 DFA 与 oracle DFA 经过 equivalence query 判别也是等价的。
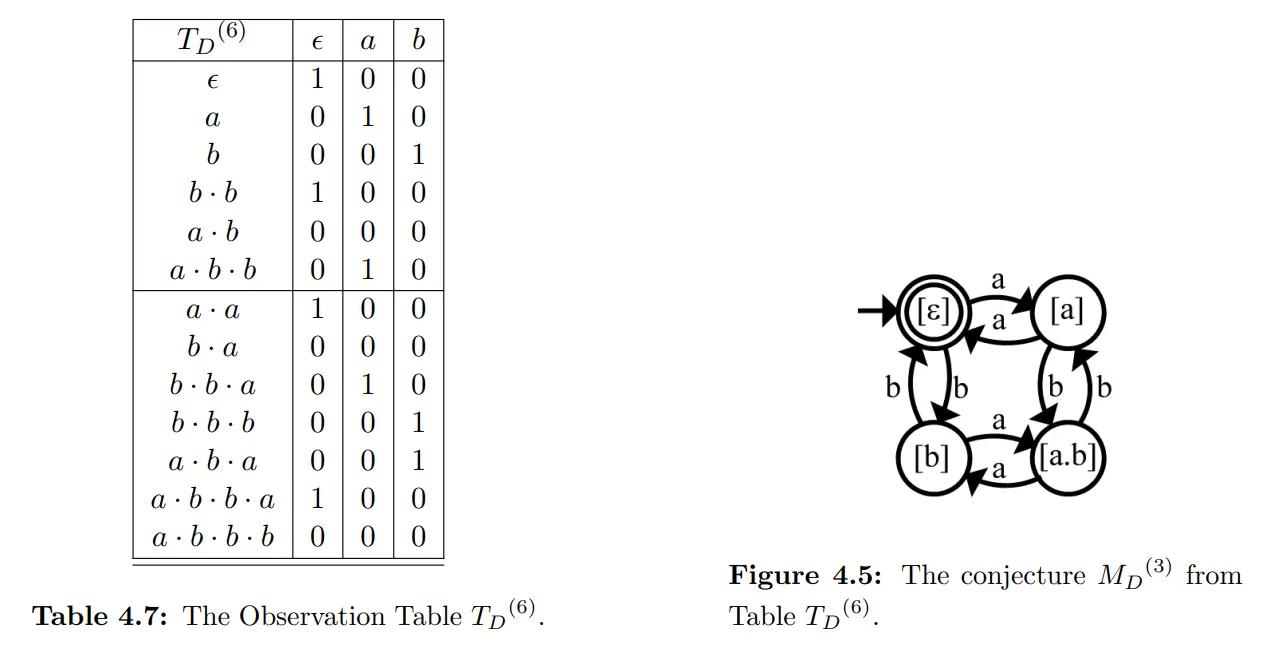
- 最终就得到了 oracle DFA 的结构。
Conclusion#
- OT 表分为上下两个部分,上半部分 用字符串(符号串)来表示,下半部分 则是用于辅助判断 的跳转目标是否已知,若已知的话应对应于某个 ,若未知则说明 中还应有新的成员。
- L* 算法学习的过程本质上是对各个状态的认识从模糊到逐步清晰的过程。
- 当 OT 不封闭时,说明需要添加新状态了,视野进一步扩大。
- 当 OT 不一致时,说明对于等价状态的认识需要进一部细化了。
- 是区分不同状态的特征值,在 DFA 中,两个状态的等价可以理解为:这两个状态分别经过相同的符号都能够跳转到终结态,或者都不能够跳转到终结态。
参考资料:
