モデル学習 Angluins' L-star アルゴリズム

DFA#

正規言語（Regular Language）の文法は、正規表現（Regular Expression）または決定性有限オートマトン（Definite Finite Automation、DFA）を用いて表現できます。例えば：

文字 a と b のみを含み、それぞれの出現回数が偶数である文字列。

は次のように表現できます。

ここで q0 は初期状態であり、終結状態でもあります。

この DFA をブラックボックスとして考え、ユーザーが文字列を入力すると、その文字列が文法に適合するかどうかのブール値（accept /reject）のみが得られます。シンボルの組み合わせを試行し、文法に適合するかどうかの判断に基づいて文法 / DFA を逆推論することは、状態モデル（state model）を学習するプロセスと見なすことができます。

Definitions, Notations#

DFA は五つ組 $(Q,\Sigma,\delta,F,q_0)$ で表されます：

$Q$ は有限のすべての可能な状態の集合。
$\Sigma$ は有限のすべての可能なシンボルの集合。
$\delta:Q\times\Sigma\rightarrow Q$ は状態遷移規則：ある状態で特定のシンボルを入力すると、オートマトンは次の状態に遷移します。
$F$ は終結状態の集合。
$q_0$ は初期状態。

Observation Table, OT#

L* アルゴリズムの核心は表 ——Observation Table（OT）であり、OT は三つ組 $(S_D,E_D,T_D)$ で表されます：

$S_D$ は接頭辞閉じた文字列の集合であり、表の行インデックスの一部です。これらの文字列は存在する可能性のある状態を表し、アクセス文字列と呼ばれます。
$E_D$ は接尾辞閉じた文字列の集合であり、表の列インデックスの集合です。これらの文字列は異なる状態を区別するために使用され（すなわち状態の同値関係を定義するため）、識別文字列と呼ばれます。OT から任意の二行 $s,t$ を取り出し、対応するすべての識別文字列の項の値が等しい場合（つまり、この二行の内容が完全に同じである場合）、これらの二行に対応する状態は同値であると記述され、 $s\cong t$ と表されます。同値の状態は 1 つの状態に統合でき、DFA では 1 つのノードとして表されます。
$T_D$ $T_{D}$ ： $(S_D \cup S_D \cdot \Sigma)\times E_D\rightarrow \{0,1\}$ $(S_{D} \cup S_{D} \cdot Σ) \times E_{D} \to {0, 1}$ は表の各行各列の項を表します。行インデックスには $S_D$ $S_{D}$ だけでなく $S_D\cdot\Sigma$ $S_{D} \cdot Σ$ も含まれ、後者は各可能な $S_D$ $S_{D}$ にシンボルを追加して構成された文字列の集合です。 $T_D(s,e)$ $T_{D} (s, e)$ の値は文字列 $s\cdot e$ $s \cdot e$ （直接接続）が accept されるかどうかによって決まり、これはブール値です。
- OT 表の中で状態を実際に表すのは $S_D$ であり、 $S_D\cdot\Sigma$ は状態間の遷移関係を判断するための補助的な役割を果たします。

OT が合理的な DFA を表すためには、二つの性質を満たす必要があります：

閉包性（closed）： $S_D\cdot\Sigma$ はある状態から出発し、シンボルを追加して到達する次の状態を表します。この新しい状態がすべての $S_D$ の状態と同値でない場合、少なくとも 1 つの新しい状態が存在することを示し、OT は閉じていないことになります。将来的に DFA を構築する際には、各状態 $S_D$ に任意のシンボル $\Sigma$ を追加した後に遷移する目的状態がわかります。目的状態が $S_D$ に既に存在する場合は問題ありませんが、存在しない場合は新しい状態がまだ探索されていないことを示します。
一貫性（consistent）：任意の二つの同値状態 $s,t\in S_D$ に対して、すべてのシンボル $i\in\Sigma$ に対して $s\cdot i\cong t\cdot i$ でなければなりません。これが成り立たない場合、s と t は同値ではなく、同じシンボルから出発して異なる状態に到達する可能性があります。同値関係は現在の OT の列インデックス（識別文字列）によって生成されるため、列インデックスに変化が生じると同値関係も変化します。一般的に、状態に対する理解は曖昧から明確へのプロセスであるため、以前は同値と見なされていた関係は、識別文字列の増加に伴い不等になることがよくあります。

L* Algorithm#

$S_D=E_D=\{\epsilon\}$ を初期化し、 $S_D\cdot\Sigma$ と共に OT のすべての行を構築します。
各行の項の値を得るために、オラクルにメンバーシップクエリを行います： $(s,e)$ に対して、オラクルに状態 s からシンボル e を経由して到達するパスが accept されるかどうかを尋ねます。表全体を埋めます。
閉包性と一貫性を判断します：
1. 閉じていない場合、 $S_D\cdot\Sigma$ から閉じていない行を一つ取り出し、 $S_D$ 部分に移動します。
2. 一貫性がない場合、すなわち $T_D(s\cdot i,e)\neq T_D(t\cdot i,e)$ の場合、 $i\cdot e$ を識別文字列に追加します。OT を横に拡張し、メンバーシップクエリを通じて表の内容を埋めます。
一貫性がある場合、OT を通じて DFA を構築し、オラクルに同値クエリを提出します：
1. 同値でない場合、オラクルは反例を返し、反例のすべての接頭辞文字列を $S_D$ に追加し、 $S_D\cdot\Sigma$ を拡張し、ステップ 2 に戻ります。
2. 同値であれば、終了します。

Example#

Reverse Engineering Enhanced State Models of Black Box Software Components to support Integration Testing に示された例の完全なプロセスは次の通りです。オラクルが次の DFA を持っていると仮定します。

その $\Sigma=\{a,b\}$ であり、 $S_D\cdot\Sigma$ は $\epsilon$ に $\Sigma$ の各シンボルを追加したもの（ ${\epsilon\cdot a,\epsilon\cdot b}$ ）で、初期状態 $q0=[\epsilon]$ です。

この OT は一貫性がありますが、閉じていません。なぜなら $\epsilon\cdot a$ が $S_D$ に同値の行（ $\epsilon\cdot b$ ）を持たないからです。そのため $\epsilon\cdot a$ （すなわち $a$ ）を $S_D$ に移動します。
a が新たに $S_D$ に追加されたため、 $S_D\cdot\Sigma$ に $a\cdot a, a\cdot b$ を追加し、オラクルにメンバーシップクエリを行い、 $T_D(a\cdot a,\epsilon)=1,\ T_D(a\cdot b,\epsilon)=0$ を得ます。
この時点で OT は閉じており、一貫性があり、同値クラスは 2 つだけです。一つは $\{\epsilon,a\cdot a\}$ 、もう一つは $\{a,b,a\cdot b\}$ であり、これらの同値クラスはグラフ上で 2 つの状態として反映され、後者のクラスに文字 a と b を追加して異なる状態に到達することで DFA を得ることができます。

この時点で同値クエリを行うと、反例 $b\cdot b$ が構築された DFA に満たされていないことがわかります。 $b\cdot b$ のすべての接頭辞（ $\{b,b\cdot b\}$ ）を OT の $S_D$ に追加し、 $b\cdot a,b\cdot b\cdot a,b\cdot b\cdot b$ を $S_D\cdot\Sigma$ に追加します。

この時点で OT は閉じていますが、一貫性がありません。なぜなら同値状態 $a,b$ が同じシンボル $a$ を追加した後の $T_D(a, a)\neq T_D(b,a)$ であるため、 $a,b$ は実際には同値ではなく、さらなる区別が必要です。区別の基準は状態 $a,b$ にシンボル $a$ を追加した後に遷移する可能性のある状態です。
$E_D$ に $a$ を追加した後、オラクルにメンバーシップクエリを行い、OT を埋めます。前の OT で同値だった a と b はこの時点で同値ではなくなっています。
この時点で OT は一貫性があり、閉じており、DFA を構築できます。

オラクルに同値クエリを行うと、反例 $a\cdot b\cdot b$ が構築された DFA が accept できるにもかかわらず、オラクルがそれを reject することがわかります。 $a\cdot b\cdot b$ のすべての接頭辞を $S_D$ に追加します（ここでは $a\cdot b\cdot b$ を追加するだけで十分です）、そして $S_D\cdot\Sigma$ に $\{a\cdot b\cdot a,a\cdot b\cdot b\cdot a,a\cdot b\cdot b\cdot b\}$ を追加します。

この時点で OT は閉じていますが、一貫性がありません。なぜなら $T_D(b,b)\neq T_D(a\cdot b,b)$ であるため、 $b$ も $E_D$ に追加する必要があり、OT を横に拡張します。
オラクル DFA にメンバーシップクエリを行い、表全体を埋めます。この時点で表は閉じており、一貫性があり、構築された DFA はオラクル DFA と同値であることが同値クエリによって確認されます。

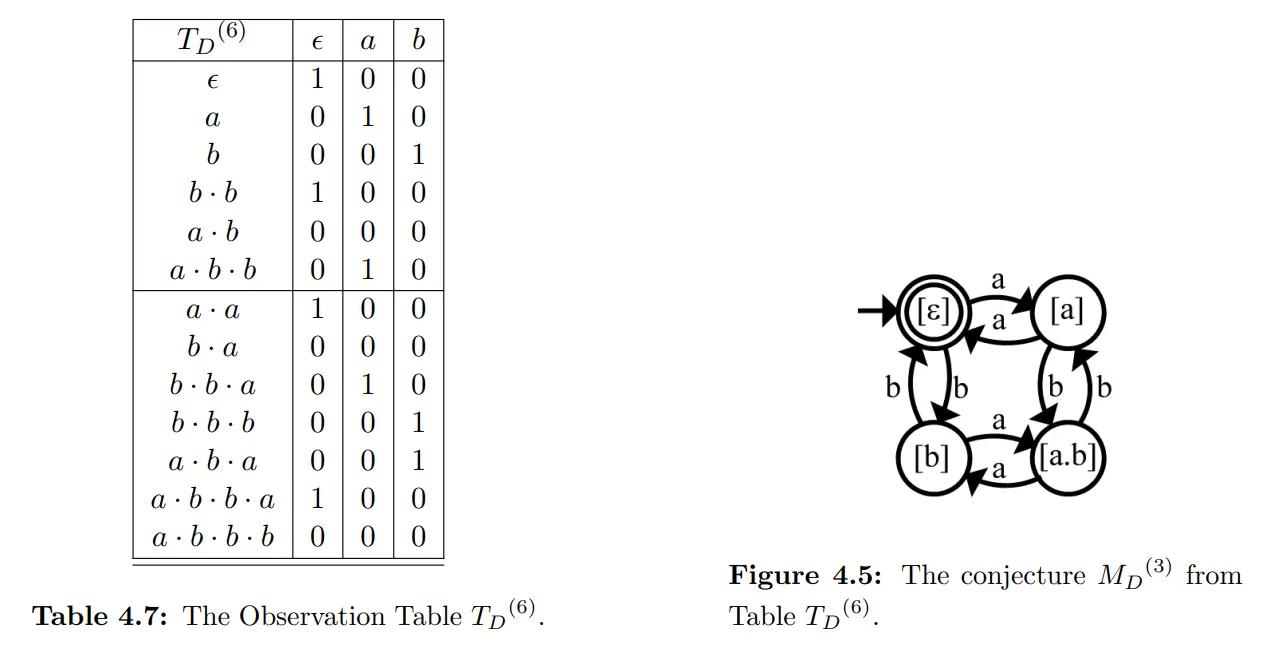
最終的にオラクル DFA の構造が得られました。

Conclusion#

OT 表は上下二つの部分に分かれています。上半分 $S_D$ は文字列（シンボル列）を用いて表現され、下半分 $S_D\cdot\Sigma$ は $S_D$ の遷移先が既知かどうかを判断するための補助的な役割を果たします。既知であれば、ある $S_D$ に対応するべきであり、未知であれば $S_D$ に新しいメンバーが存在することを示します。
L* アルゴリズムの学習プロセスは、本質的に各状態の理解が曖昧から徐々に明確になるプロセスです。
- OT が閉じていない場合、新しい状態を追加する必要があることを示し、視野がさらに広がります。
- OT が一貫性がない場合、同値状態の理解をさらに詳細にする必要があることを示します。
$E_D$ は異なる状態を区別する特徴値であり、DFA において二つの状態の同値は、これら二つの状態がそれぞれ同じシンボルを経由して終結状態に遷移できるか、またはどちらも終結状態に遷移できないことを理解できます。

参考資料：